二元期权组合
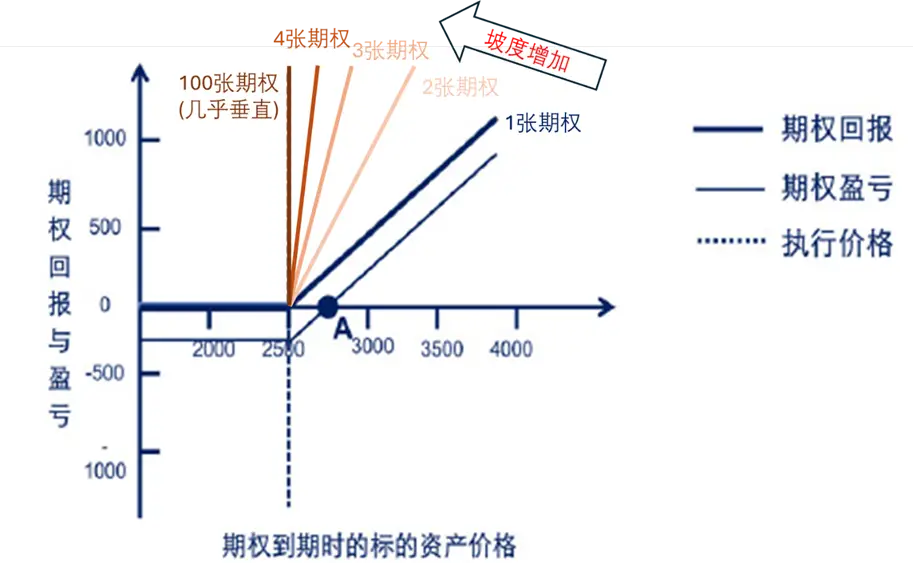
从图三可见,一张看涨香草期权价格与到期时的底层资产价格成一比一的线性关系。换言之,持有一张在价内的期权,能够为持有者带来与底层资产价格变化成一比一的收益;持有两张价内的期权,能为持有者带来与底层资产价格变化成一比二的收益,让其损益分布图的线性坡度变得更陡(图四),以此类推。如果期权的数量足够多,便能实现接近垂直的坡度,大幅强化投资者收益。虽然此结构能创造夸张的收益,但购买如此大量的价内期权成本非常高。
图四、组合回报坡度与香草期权数量成正比
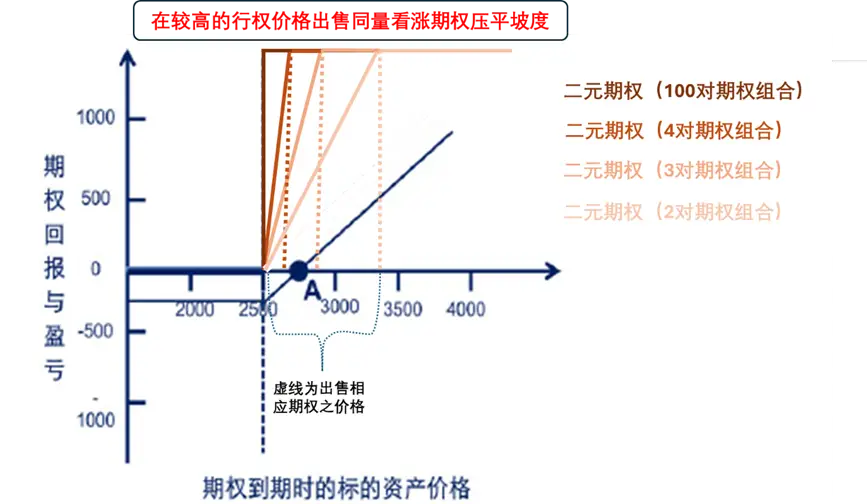
为控制成本,投资者可以在稍高的行权价格(看跌香草期权便是稍低的行权价格)售出同量的看涨香草期权(看跌则为看跌香草期权)。由于两张期权的行权价格非常接近,出售期权的收入几乎能与买入期权的成本抵消,投资者只需付【两张不同行权价格的期权价差*期权数量】便能获得断层式的组合回报,又称二元期权(图五)。
图五、二元期权回报示意图
二元期权应用
二元期权的独特回报能让看好/看坏某事情发生的投资者,在二元结果里获得一个固定的收入的回报,因此也称固定收益期权。此回报结构广泛在不同结构化票据中使用,如区间计息票据和单鲨票据等,提供投资者对赌某事件发生(或不发生)的机会。
以香草期权组合模拟出来的二元期权有一定的风险。如果挂钩标的的价格掉进了两张期权的行权价中间,投资者或面临非二元回报(线性回报)。因此,在使用香草期权模拟二元期权时,需尽量减少两张期权行权价中间的差额,并用多张期权提高坡度和回报。
二元期权定价
二元期权的定价可以用以下两种方法:
1. 无套利定价
二元期权的估价最直接的方式是用无套利定价原理,计算回报模拟组合(香草期权组合)的总成本。做法是从市场询得看涨香草期权的市价,并计算以上回报模拟组合的净成本。
2. 布萊克-休斯模型定价 (Black-Scholes Model)
布萊克-休斯模型为传统的期权定价模型,其定价并不依赖期权市场资讯,而是底层资产价格以及年化波动,能够在缺乏期权市场价格的情况下为票据定价。
*本文所有期权均为欧式期权
以下为以香草期权组合出二元期权的示例:
二元期权的回报示意图及解构
回报为8.5%,行权价格为 1.0% 的美国SOFR利率看涨二元期权。
